XYZ表色系

さてさて、XYZ表色系きましたよ。

こいつは強敵ですね。他の項目では割と「実は簡単です」とかありますが、XYZ表色系は普通によくわからん。一つの原因として、マンセルのような顕色系のカラーシステムと違って、式を使って数値で色をはじき出すので、とても抽象度が高いんですよね。イメージしにくい。

とはいえ、こいつはいつかは倒さなくてはいけないヤツなので、小分けにしてゆっくりでも、少しずつ理解を進めていきましょう。

なにせ、とても優秀な表色系です。

光源色（光源からの光）も物体色（物体によって吸収反射した光）も含めてありとあらゆるすべての色を、数値でピンポイントで指定することができるのです。研究や開発に欠かせないシステムであることが想像できるでしょう。

XYZの三刺激値

全ての色は、三原色を特定に比率で混ぜ合わせてあげる（加法混色）ことで表現することが可能でしたね。グラスマンの「色の三色性」ですね。式は覚えていますか？ 

色光[C] ≡ R[R] + G[G] + B[B]

でした。

XYZ表色系では、その表色系名の通り、色をX、Y、Zという原刺激を用いて三刺激値を

色光[C] ≡ X[X] + Y[Y] + Z[Z]

と表しています。しかし、一つ問題が発生があります。

実際に色光を重ね合わせていくと、白に向かうにつれて色の彩度が低下していきます。（……まあ、上の三原色図では低下していないんですが。）

よって、混ぜ合わせる色の比率にマイナスの値を使う必要が出てきます。これは色図上に三原色によって作られる三角形より外側にも色があることからも理解できるので、もうちょっとお待ちください。

とにかく、このマイナスの値問題を解決するために、XYZ表色系は、

• 加法混色に置いて全ての色をマイナスを使わずに表せること
• 原刺激[X]は赤み、原刺激[Z]は青み、原刺激[Y]は緑みと明るさを持つ

といった考えの元で作られています。

色度座標

X、Y、Zの3つの刺激値で色を表すのがXYZ表色系です。

しかし、マンセル表色系なんかと違って3つの刺激値を言われても、実際に混ぜ合わせた時にどのような色になるのか非常に想像しにくい、という欠点があります。

そこで、色光[C]を表すこの式、

色光[C] ≡ X[X] + Y[Y] + Z[Z]

この、X、Y、Zのそれぞれを混ぜ合わせる比率で表現してしまおう、ということになりました。混色系の表色系では、この3色の混合比率を指定してあげることで、特定の値を表します。

目的の色C ≡  色Xの割合 ＋色Yの割合 ＋ 色Zの割合

ということですね。この比率は、目的の色を作り出す3つの色の比率です。XYZ表式系では、XYZの値を全て足すと「1」になるように割合の値を指定します。

この3つの原刺激の比率を座標軸で表したものを「色度座標」と言います。

3つの値の座標なのだから3次元空間になるのかな……？ と思うかもしれません。しかし、この3つの値は「1」に対する比率なので、3つのうち2つの値が決まれば最後の当たりも確定します。よって色度座標はＸ、Ｙの2次元のマップで表すことが可能です。

例えば「マンセル値 5R 4/14」の赤を色度座標で表すと、

x = 0.5734, y = 0.33

となります。

xy色度図

ちょっと文章や式ばかりだとイメージするのがつらいので、xy色度座標を平面上に表した「色度図」を見ていきましょう。

縦がx、横がyとなっています。

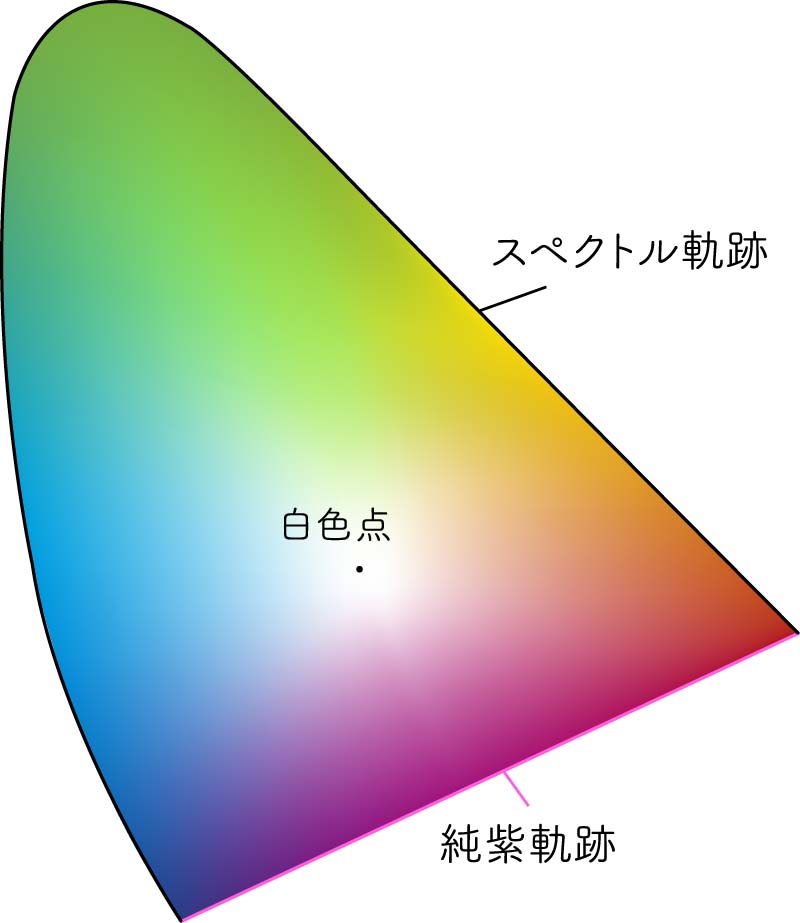
横軸xの値が大きくなればなるほど、色は赤みを増し、縦軸yの値が大きくなればなるほど緑みが増すのが分かりますね。では、省かれてしまったz、つまり青みを増すにはどうしたらよいか、というと、x/y両方の値を小さくすれば、相対的にzの値が大きくなりますね。よくできています。

この馬のひづめのような形をした色空間で、半円を書くように丸くなっている曲線を「スペクトル軌跡」と言います。辿っていけば分かりますが、スペクトル色（可視光線の波長の色、つまり虹の色）になていますね。また、スペクトル軌跡の反対側の赤と紫を結んだ直線を「純紫軌跡」といいます。赤と紫を混ぜ合わせた、スペクトル色には存在しない色のラインですね。

R、G、Ｂの色を同じ比率で混ぜ合わせると無彩色になります。原刺激[X]を0.33、原刺激[Y]を0.33（そして必然的に原刺激[Z]が0.33）混ぜ合わせるた時に、色は完全な無彩色となります。それが「白色点」といわれるポイントです。

あれ、黒色点はないの？ と思ったかもしれませんが、xy色度図で表現するのはあくまで「色相」と「彩度」のみです。明度は表していません。